Arnold Beckmann - "Cut-reduction by switching"
Abstract:
|
Usual cut-elimination procedures like the Gentzen- or
Tait-style cut elimination methods have the cost of a (super-)
exponential increase of the size of derivations. Cut-reduction
by switching utilises methods from Boolean complexity to reduce
the complexity of cuts in a derivation without increasing the
size of the derivation. However, the disadvantage is that not
only is the complexity of cut formulas reduced, but also the
complexity of the derived formula.
In this talk I will explain Cut-reduction by switching and the
use of Sipser functions to rescue the derived formula. I will
point out applications of cut-reduction by switching, which will
mainly be in the area of propositional proof systems [1].
Jan Krajicek [2] was the first one who used such methods from
Boolean complexity in this setting.
[1] J.Krajicek: Lower bounds to the size of constant-depth
Frege proofs. JSL, 59:73-86, 1994.
[2] A.Beckmann and S.Buss: Separation results for the size of
constant-depth propositional proofs. To appear in APAL.
|
Lev Beklemishev - "On Schmerl's reduction formula and its relation to cut-elimination"
Abstract:
|
Schmerl's reduction formula states that, in the context of formal
arithmetic, a reflection principle of logical complexity 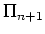 can can
be conservatively approximated by finitely iterated reflection principles
of complexity 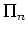 . It can be seen as an analog of the cut-elimination . It can be seen as an analog of the cut-elimination
theorem for omega-logic. However, there are some notable differences. In
the talk we shall compare the two results.
|
Agata Ciabattoni - "Towards a semantic characterization of cut-elimination"
(joint work with. K. Terui)
Abstract:
|
We introduce necessary and sufficient conditions for a
(single-conclusion) sequent calculus to admit
cut-elimination. Our conditions are formulated both syntactically and
semantically.
|
Rosalie Iemhoff - "Truth value logics and the existence predicate"
Abstract:
|
We introduce Scott logics, which are generalizations of Gödel
logics that correspond in the same manner to the logics of linear
frames as Gödel logics correspond to the logics of linear frames
with constant domains. This correspondence result is based on
previous results by A. Beckamnn and N. Preining. We discuss the
relation to the existence predicate and show that this predicate
enables us to define a faithful translation of Scott logics into
Gödel logics.
|
George Metcalfe - "Density Elimination"
Abstract:
Grigori Mints - "Cut elimination for provability logic"
Abstract:
|
Provability logic is one of the most popular modal logics. It is sound
and complete for the interpretation of modality as provabiulity in
Peano Arithmetic and many other theories.
It turns out that there is no accepted syntactic cut elimination
(normalization) proof for a standard sequent formulation of the provability
logic. A proof by D. Leivant in [1] contained a
gap, subsequent proof by S. Valentini [2] was also
incomplete. A model-theoretic proof of the normal form theorem along
the familiar lines was given by several authors.
We present a syntactic cut elimination proof along the standard
lines. The main step absent in previous papers is the cut-free
admissibility of the rule
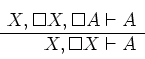
[1] Leivant.
[2] Valentini.
|
Georg Moser - "Ackermann's Substitution Method (remixed)"
Abstract:
Pavel Pudlák - "On the structure of terms in Herbrand's disjunctions"
Abstract:
|
The basic information concerning Herbrand's disjunctions is
in which terms which variables occur. This structure determines
whether, given a disjunction of term-instances of an open formula, one
can derive a first order sentence with a particular quantifier
prefix. We shall study this dependence using a two player game with
players corresponding to the two quantifiers. Then the structure is
determined by the ordering of the moves of the two players. The main
problem that we address in the lecture is to find a class of orderings
which is as small as possible and such that all logically valid
sentences of a given quantifier prefix have Herbrand proofs with such
orderings.
|
Clemens Richter - "Cut-Elimination: Experiments with CERES"
Abstract:
|
Cut-elimination is the most prominent form of proof transformation
in logic. The elimination of cuts in formal proofs corresponds to
the removal of intermediate statements (lemmas) in mathematical
proofs. The cut-elimination method CERES (cut-elimination by
resolution) works by constructing a set of clauses
from a proof with cuts. Any resolution refutation of this set can
then serve as a skeleton of a proof with only atomic cuts.
In this talk we present an implementation of CERES, in particular
the basic algorithms, the input format and the integration of the
well-known automated theorem prover 'Otter'. Furthermore a systematic
experiment with the implementation of CERES on a proof of reasonable
size and complexity will be presented. It turns out
that the proof with cuts can be transformed into two "mathematically"
different proofs of the theorem. In particular, the application of
positive
and negative hyperresolution yield different mathematical arguments.
As an unexpected side-effect the derived clauses of the resolution
refutation proved particularly interesting as they can be considered
as meaningful universal lemmas.
Though the proof under investigation is intuitively simple, the
experiment demonstrates that new (and relevant) mathematical
information on proofs can be obtained by computational methods. It
can be considered as a first step in the development of an
experimental culture of "computer-aided proof analysis" in
mathematics.
|
Helmut Schwichtenberg - "Program Extraction from Normalization Proofs"
(joint work with Ulrich Berger and Pierre Letouzey)
Abstract:
|
We formalize Tait's proof of the existence of normal forms for terms
of the simply typed lambda-calculus, and machine-extract a program
from this proof, which turns out to implement the well-known
normalization by evaluation algorithm.
On paper, this has already been done by Ulrich Berger (TLCA 1993).
However -- as is to be expected -- the formalization turned out to be
not at all a trivial matter, so that it appears to be worthwhile to
describe some of the choices which have simplified the task
considerably. On the other hand, a full formalization is
necessary for machine extraction of a program from such a proof.
We carry this out for the proof assistant Minlog which has a suitable
program extraction machinery built in. This provides a useful
occasion to test this machinery in a non-trivial setting.
|
Christian Urban - "On the Cambridge Interpretation of Cut-Elimination in Classical Logic"
Abstract:
|
It is a familiar idea that in intuitionistic logic one can interpret the
process of normalisation, and hence also cut-elimination, as computation in
the lambda-calculus. There have been many proposals to obtain a similar
interpretation for nomalisation and cut-elimination in classical logic.
In the talk I will give an overview about the ideas a group of people had in
Cambridge concerning the computational content of classical proofs. The
starting point for this overview is a strongly normalising cut-elimination
procedure for classical logic. This cut-elimination procedure provides a
unifying framework in which the existing proposals can be embedded and in
which one can experiment with many phenomena of cut-elimination in classical
logic. I will discuss how far we have come in Cambridge and where we
failed to provide clear cut results.
|