Assume a deduction system I based on resolution. To prove the validity of F, not F is transformed into a sat-equivalent clause set C, To keep our argumentation simple, we assume C to be decidable by I If I is applied on C, then it terminates with a saturated set of clauses C' not containing the empty clause. Provided I is refutationally complete, C' is consistent. Hence, the set C represents a (possibly infinite) class of counter-examples, but it is usually not possible to extract one of these models of C' directly. In most cases it is not even possible to extract an `understandable' model representation of one of these models.The goal of our approach to Automated Model Building is to transform C' into a representation of an (infinite) Herbrand model of \C. We call this representation model representation.
No hungry cat gazes at the moon. Some cats gazing at the moon are in love. Conclude that some cats which are in love are hungry.There are arbitrarily many possibilities to modify a statement so that it becomes valid. If we decide that our premises are correct, we have to reconsider the conclusion:
We want to know whether the conclusion is logically justified or not.
Let "H(x)" stand for "x is a hungry cat", "G(x)" for "cat x gazes at the moon", and "L(x)" for "cat x is in love". Now, we encode our problem in first-order logic:F <-> [(forall x)( H(x) -> not G(x)) and (exists x)( G(x) and L(x))] -> (exists x)( L(x) and H(x)).
To apply resolution, we have to transform not F into a clause set
C= {not H(x) or not G(x), G(a), L(a), not L(x) or not H(x) }
It is easy to see that any reasonable resolution refinement terminates on C, without inferring the empty clause. If we want to correct F such that it becomes valid, the counter-example (assuming, we can actually construct one), can serve as guiding data. With the methods employed in TILT the following Herbrand model I = { not H(a), G(a), L(a) } is derivable. This models describes a word in which exists exactly one cat a, this cat is in love, free of hunger and gazing at the moon.
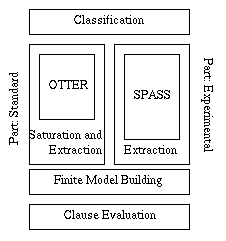
No hungry cat gazes at the moon. Some cats gazing at the moon are in love. Conclude that some cats which are in love are {\em not} hungry.The deduction system TILT implements the recent results of the Vienna Group. TILT embodies three components
We denote the corresponding formula as F'. Applying resolution to the new clause set C', sat-equivalent to not F', we derive the empty clause. Hence, the new conclusion is justified. We call this approach to Automated Model building resolution-based.
